









试读已结束,还剩9页未读,您可下载完整版后进行离线阅读
《2015年浙江省高考数学(理科)试卷word版+(含答案)》是由用户上传到老师板报网,本为文库资料,大小为475.5 KB,总共有19页,格式为doc。授权方式为VIP用户下载,成为老师板报网VIP用户马上下载此课件。文件完整,下载后可编辑修改。
- 文库资料
- 19页
- 475.5 KB
- VIP模板
- doc
- 数字产品不支持退货
2015年浙江省高考数学试卷(理科) 一、选择题:本大题共8小题,每小题5分,共40分2015年普通高等学校招生全国统一考试(浙江卷)数学(理科)1.(5分)(2015•浙江)已知集合P={x|x22x≥0}﹣,Q={x|1<x≤2},则(∁RP)∩Q=( ) A.[0,1)B.(0,2]C.(1,2)D.[1,2] 2.(5分)(2015•浙江)某几何体的三视图如图所示(单位:cm),则该几何体的体积是( ) A.8cm3B.12cm3C.D. 3.(5分)(2015•浙江)已知{an}是等差数列,公差d不为零,前n项和是Sn,若a3,a4,a8成等比数列,则( ) A.a1d>0,dS4>0B.a1d<0,dS4<0C.a1d>0,dS4<0D.a1d<0,dS4>0 4.(5分)(2015•浙江)命题“∀n∈N*,f(n)∈N*且f(n)≤n”的否定形式是( ) A.∀n∈N*,f(n)∉N*且f(n)>nB.∀n∈N*,f(n)∉N*或f(n)>n C.∃n0∈N*,f(n0)∉N*且f(n0)>n0D.∃n0∈N*,f(n0)∉N*或f(n0)>n0 5.(5分)(2015•浙江)如图,设抛物线y2=4x的焦点为F,不经过焦点的直线上有三个不同的点A,B,C,其中点A,B在抛物线上,点C在y轴上,则△BCF与△ACF的面积之比是( ) A.B.C.D. 6.(5分)(2015•浙江)设A,B是有限集,定义:d(A,B)=card(AB∪)﹣card(A∩B),其中card(A)表示有限集A中的元素个数( )命题①:对任意有限集A,B,“A≠B”是“d(A,B)>0”的充分必要条件;命题②:对任意有限集A,B,C,d(A,C)≤d(A,B)+d(B,C) A.命题①和命题②都成立B.命题①和命题②都不成立 C.命题①成立,命题②不成立D.命题①不成立,命题②成立 7.(5分)(2015•浙江)存在函数f(x)满足,对任意x∈R都有( ) A.f(sin2x)=sinxB.f(sin2x)=x2+xC.f(x2+1)=|x+1|D.f(x2+2x)=|x+1| 8.(5分)(2015•浙江)如图,已知△ABC,D是AB的中点,沿直线CD将△ACD折成△A′CD,所成二面角A′CDB﹣﹣的平面角为α,则( ) A.A′DB≤α∠B.A′DB≥α∠C.A′CB≤α∠D.A′CB≥α∠ 二、填空题:本大题共7小题,多空题每题6分,单空题每题4分,共36分.9.(6分)(2015•浙江)双曲线=1的焦距是 ,渐近线方程是 . 10.(6分)(2015•浙江)已知函数f(x)=,则f(f(﹣3))=,f(x)的最小值是 . 11.(6分)(2015•浙江)函数f(x)=sin2x+sinxcosx+1的最小正周期是 ,单调递减区间是 . 12.(4分)(2015•浙江)若a=log43,则2a+2a﹣= . 13.(4分)(2015•浙江)如图,三棱锥ABCD﹣中,AB=AC=BD=CD=3,AD=BC=2,点M,N分别是AD,BC的中点,则异面直线AN,CM所成的角的余弦值是 . 14.(4分)(2015•浙江)若实数x,y满足x2+y2≤1,则|2x+y2|+|6x3y|﹣﹣﹣的最小值是. 15.(6分)(2015•浙江)已知是空间单位向量,,若空间向量满足,且对于任意x,y∈R,,则x0= ,y0= ,|= . 三、解答题:本大题共5小题,共74分.解答应写出文字说明、证明过程或演算步骤.16.(14分)(2015•浙江)在△ABC中,内角A,B,C所对的边分别为a,b,c,已知A=,b2a﹣2=c2.(1)求tanC的值;(2)若△ABC的面积为3,求b的值. 17.(15分)(2015•浙江)如图,在三棱柱ABCA﹣1B1C1中,∠BAC=90°,AB=AC=2,A1A=4,A1在底面ABC的射影为BC的中点,D是B1C1的中点.(1)证明:A1D⊥平面A1BC;(2)求二面角A1BDB﹣﹣1的平面角的余弦值. 18.(15分)(2015•浙江)已知函数f(x)=x2+ax+b(a,b∈R),记M(a,b)是|f(x)|在区间[1﹣,1]上的最大值.(1)证明:当|a|≥2时,M(a,b)≥2;(2)当a,b满足M(a,b)≤2时,求|a|+|b|的最大值. 19.(15分)(2015•浙江)已知椭圆上两个不同的点A,B关于直线y=mx+对称.(1)求实数m的取值范围;(2)求△AOB面积的最大值(O为坐标原点). 20.(15分)(2015•浙江)已知数列{an}满足a1=且an+1=ana﹣n2(n∈N*)(1)证明:1≤≤2(n∈N*);(2)设数列{an2}的前n项和为Sn,证明(n∈N*). 2015年浙江省高考数学试卷(理科)参考答案与试题解析 一、选择题:本大题共8小题,每小题5分,共40分2015年普通高等学校招生全国统一考试(浙江卷)数学(理科)1.(5分)考点:交、并、补集的混合运算.菁优网版权所有专题:集合.分析:求出P中不等式的解集确定出P,求出P补集与Q的交集即可.解答:解:由P中不等式变形得:x(x2﹣)≥0,解得:x≤0或x≥2,即P=(﹣∞,0][2∪,+∞),∴∁RP=(0,2),Q=∵(1,2],∴(∁RP)∩Q=(1,2),故选:C.点评:此题考查了交、并、补集的混合运算,熟练掌握运算法则是解本题的关键.2.(5分)考点:由三视图求面积、体积.菁优网版权所有专题:空间位置关系与距离.分析:判断几何体的形状,利用三视图的数据,求几何体的体积即可.解答:解:由三视图可知几何体是下部为棱长为2的正方体,上部是底面为边长2的正方形奥为2的正四棱锥,所求几何体的体积为:23+×2×2×2=.故选:C.点评:本题考查三视图与直观图的关系的判断,几何体的体积的求法,考查计算能力. 3.(5分)考点:等差数列与等比数列的综合.菁优网版权所有专题:等差数列与等比数列.分析:由a3,a4,a8成等比数列,得到首项和公差的关系,即可判断a1d和dS4的符号.解答:解:设等差数列{an}的首项为a1,则a3=a1+2d,a4=a1+3d,a8=a1+7d,由a3,a4,a8成等比数列,得,整理得:.d≠0∵,∴,∴,=<0.故选:B.点评:本题考查了等差数列和等比数列的性质,考查了等差数列的前n项和,是基础题.4.(5分)考点:命题的否定.菁优网版权所有专题:简易逻辑.分析:根据全称命题的否定是特称命题即可得到结论.解答:解:命题为全称命题,则命题的否定为:∃n0∈N*,f(n0)∉N*或f(n0)>n0,故选:D.点评:本题主要考查含有量词的命题的否定,比较基础. 5.(5分)考点:直线与圆锥曲线的关系.菁优网版权所有专题圆锥曲线的定义、性质与方程.:分析:根据抛物线的定义,将三角形的面积关系转化为的关系进行求解即可.解答:解:如图所示,抛物线的准线DE的方程为x=1﹣,过A,B分别作AEDE⊥于E,交y轴于N,BDDE⊥于E,交y轴于M,由抛物线的定义知BF=BD,AF=AE,则|BM|=|BD|1=|BF|1﹣﹣,|AN|=|AE|1=|AF|1﹣﹣,则===,故选:A点评:本题主要考查三角形的面积关系,利用抛物线的定义进行转化是解决本题的关键. 6.(5分)考点:复合命题的真假.菁优网版权所有专题:集合;简易逻辑.分析:命题①根据充要条件分充分性和必要性判断即可,③借助新定义,根据集合的运算,判断即可.解答:解:命题①:对任意有限集A,B,若“A≠B”,则AB≠A∩B∪,则card(AB∪)>card(A∩B),故“d(A,B)>0”成立,若d(A,B)>0”,则card(AB∪)>card(A∩B),则AB≠A∩B∪,故A≠B成立,故命题①成立,命题②,d(A,B)=card(AB∪)﹣card(A∩B),d(B,C)=card(BC∪)﹣card(B∩C),d∴(A,B)+d(B,C)=card(AB∪)﹣card(A∩B)+card(BC∪)﹣card(B∩C)=[card(AB∪)+card(BC∪)][card﹣(A∩B)+card(B∩C)]≥card(AC∪)﹣card(A∩C)=d(A,C),故命题②成立,故选:A点评:本题考查了,元素和集合的关系,以及逻辑关系,分清集合之间的关系与各集合元素个数之间的关系,注意本题对充要条件的考查.集合的元素个数,体现两个集合的关系,但仅凭借元素个数不能判断集合间的关系,属于基础题. 7.(5分)考点:函数解析式的求解及常用方法.菁优网版权所有专题:函数的性质及应用.分析:利用x取特殊值,通过函数的定义判断正误即可.解答:解:A.取x=0,则sin2x=0,∴f(0)=0;取x=,则sin2x=0,∴f(0)=1;f∴(0)=0,和1,不符合函数的定义;∴不存在函数f(x),对任意x∈R都有f(sin2x)=sinx;B.取x=0,则f(0)=0;取x=π,则f(0)=π2+π;f∴(0)有两个值,不符合函数的定义;∴该选项错误;C.取x=1,则f(2)=2,取x=1﹣,则f(2)=0;这样f(2)有两个值,不符合函数的定义;∴该选项错误;D.令|x+1|=t,t≥0,则f(t21﹣)=t;令t21=x﹣,则t=;∴;即存在函数f(x)=,对任意x∈R,都有f(x2+2x)=|x+1|;∴该选项正确.故选:D.点评:本题考查函数的定义的应用,基本知识的考查,但是思考问题解决问题的方法比较难. 8.(5分)考点:二面角的平面角及求法.菁优网版权所有专题:创新题型;空间角.分析解:画出图形,分AC=BC,AC≠BC两种情况讨论即可.:解答:解:①当AC=BC时,∠A′DB=α;②当AC≠BC时,如图,点A′投影在AE上,α=A′OE∠,连结AA′,易得∠ADA′<∠AOA′,A′DB∴∠>∠A′OE,即∠A′DB>α综上所述,∠A′DB≥α,故选:B.点评:本题考查空间角的大小比较,注意解题方法的积累,属于中档题. 二、填空题:本大题共7小题,多空题每题6分,单空题每题4分,共36分.9.(6分)考点:双曲线的简单性质.菁优网版权所有专题:计算题;圆锥曲线的定义、性质与方程.分析:确定双曲线中的几何量,即可求出焦距、渐近线方程.解答:解:双曲线=1中,a=,b=1,c=,∴焦距是2c=2,渐近线方程是y=±x.故答案为:2;y=±x.点评:本题考查双曲线的方程与性质,考查学生的计算能力,比较基础.10.(6分)考点:函数的值.菁优网版权所有专题计算题;函数的性质及应用.:分析:根据已知函数可先求f(﹣3)=1,然后代入可求f(f(﹣3));由于x≥1时,f(x)=,当x<1时,f(x)=lg(x2+1),分别求出每段函数的取值范围,即可求解解答:解:∵f(x)=,f∴(﹣3)=lg10=1,则f(f(﹣3))=f(1)=0,当x≥1时,f(x)=,即最小值,当x<1时,x2+1≥1,(x)=lg(x2+1)≥0最小值0,故f(x)的最小值是.故答案为:0;.点评:本题主要考查了分段函数的函数值的求解,属于基础试题.11.(6分)考点:两角和与差的正弦函数;三角函数的周期性及其求法;正弦函数的单调性.菁优网版权所有专题:三角函数的求值.分析:由三角函数公式化简可得f(x)=sin(2x﹣)+,易得最小正周期,解不等式2kπ+≤2x﹣≤2kπ+可得函数的单调递减区间.解答:解:化简可得f(x)=sin2x+sinxcosx+1=(1cos2x﹣)+sin2x+1=sin(2x﹣)+,∴原函数的最小正周期为T==π,由2kπ+≤2x﹣≤2kπ+可得kπ+≤x≤kπ+,∴函数的单调递减区间为[kπ+,kπ+](k∈Z)故答案为:π;[kπ+,kπ+](k∈Z)点评:本题考查三角函数的化简,涉及三角函数的周期性和单调性,属基础题.12.(4分)考点:对数的运算性质.菁优网版权所有专题:函数的性质及应用.分析:直接把a代入2a+2a﹣,然后利用对数的运算性质得答案.解答:解:∵a=log43,可知4a=3,即2a=,所以2a+2a﹣=+=.故答案为:.点评:本题考查对数的运算性质,是基础的计算题.13.(4分)考点:异面直线及其所成的角.菁优网版权所有专题:空间角.分析:连结ND,取ND的中点为:E,连结ME说明异面直线AN,CM所成的角就是∠EMC通过解三角形,求解即可.解答:解:连结ND,取ND的中点为:E,连结ME,则MEAN∥,异面直线AN,CM所成的角就是∠EMC,AN=2∵,ME=∴=EN,MC=2,又∵ENNC⊥,∴EC==,cosEMC=∴∠==.故答案为:.点评:本题考查异面直线所成角的求法,考查空间想象能力以及计算能力.14.(4分)考点:函数的最值及其几何意义.菁优网版权所有专题:不等式的解法及应用;直线与圆.分析:根据所给x,y的范围,可得|6x3y|=6x3y﹣﹣﹣﹣,再讨论直线2x+y2=0﹣将圆x2+y2=1分成两部分,分别去绝对值,运用线性规划的知识,平移即可得到最小值.解答:解:由x2+y2≤1,可得6x3y﹣﹣>0,即|6x3y|=6x3y﹣﹣﹣﹣,如图直线2x+y2=0﹣将圆x2+y2=1分成两部分,在直线的上方(含直线),即有2x+y2≥0﹣,即|2+y2|=2x+y2﹣﹣,此时|2x+y2|+|6x3y|=﹣﹣﹣(2x+y2﹣)+(6x3y﹣﹣)=x2y+4﹣,利用线性规划可得在A(,)处取得最小值3;在直线的下方(含直线),即有2x+y2≤0﹣,即|2+y2|=﹣﹣(2x+y2﹣),此时|2x+y2|+|6x3y|=﹣﹣﹣﹣(2x+y2﹣)+(6x3y﹣﹣)=83x4y﹣﹣,利用线性规划可得在A(,)处取得最小值3.综上可得,当x=,y=时,|2x+y2|+|6x3y|﹣﹣﹣的最小值为3.故答案为:3.点本题考查直线和圆的位置关系,主要考查二元函数在可行域内取得最值的方法,属于中档评:题.15.(6分)考点:空间向量的数量积运算;平面向量数量积的运算.菁优网版权所有专题:创新题型;空间向量及应用.分析:由题意和数量积的运算可得<•>=,不妨设=(,,0),=(1,0,0),由已知可解=(,,t),可得|﹣(|2=(x+)2+(y2﹣)2+t2,由题意可得当x=x0=1,y=y0=2时,(x+)2+(y2﹣)2+t2取最小值1,由模长公式可得|.解答:解:∵•=||||cos<•>=cos<•>=,∴<•>=,不妨设=(,,0),=(1,0,0),=(m,n,t),则由题意可知=m+n=2,=m=,解得m=,n=,∴=(,,t),∵﹣()=(﹣xy﹣,,t),|∴﹣(|2=(﹣xy﹣)2+()2+t2=x2+xy+y24x5y+t﹣﹣2+7=(x+)2+(y2﹣)2+t2,由题意当x=x0=1,y=y0=2时,(x+)2+(y2﹣)2+t2取最小值1,此时t2=1,故|==2故答案为:1;2;2点评:本题考查空间向量的数量积,涉及向量的模长公式,属中档题. 三、解答题:本大题共5小题,共74分.解答应写出文字说明、证明过程或演算步骤.16.(14分)考点:余弦定理.菁优网版权所有专题:解三角形.分析:(1)由余弦定理可得:,已知b2a﹣2=c2.可得,a=.利用余弦定理可得cosC.可得sinC=,即可得出tanC=.(2)由=×=3,可得c,即可得出b.解答:解:(1)∵A=,∴由余弦定理可得:,∴b2a﹣2=bcc﹣2,又b2a﹣2=c2.∴bcc﹣2=c2.∴b=c.可得,a∴2=b2﹣=,即a=.cosC=∴==.C∵∈(0,π),sinC=∴=.tanC=∴=2.(2)∵=×=3,解得c=2.∴=3.点评:本题考查了正弦定理余弦定理、同角三角形基本关系式、三角形面积计算公式,考查了推理能力与计算能力,属于中档题.17.(15分)考点:二面角的平面角及求法;直线与平面垂直的判定.菁优网版权所有专题:空间位置关系与距离;空间角.分析:(1)以BC中点O为坐标原点,以OB、OA、OA1所在直线分别为x、y、z轴建系,通过•=•=0及线面垂直的判定定理即得结论;(2)所求值即为平面A1BD的法向量与平面B1BD的法向量的夹角的余弦值的绝对值的相反数,计算即可.解答(1)证明:如图,以BC中点O为坐标原点,以OB、OA、OA1所在直线分别为x、y、z轴建系.:则BC=AC=2,A1O==,易知A1(0,0,),B(,0,0),C(﹣,0,0),A(0,,0),D(0,﹣,),B1(,﹣,),=(0,﹣,0),=(﹣,﹣,),=(﹣,0,0),=(﹣2,0,0),=(0,0,),∵•=0,∴A1DOA⊥1,又∵•=0,∴A1DBC⊥,又∵OA1∩BC=O,∴A1D⊥平面A1BC;(2)解:设平面A1BD的法向量为=(x,y,z),由,得,取z=1,得=(,0,1),设平面B1BD的法向量为=(x,y,z),由,得,取z=1,得=(0,,1),cos∴<,>===,又∵该二面角为钝角,∴二面角A1BDB﹣﹣1的平面角的余弦值为﹣.点评:本题考查空间中线面垂直的判定定理,考查求二面角的三角函数值,注意解题方法的积累,属于中档题. 18.(15分)考点:二次函数在闭区间上的最值.菁优网版权所有专题:函数的性质及应用.分析:(1)明确二次函数的对称轴,区间的端点值,由a的范围明确函数的单调性,结合已知以及三角不等式变形所求得到证明;(2)讨论a=b=0以及分析M(a,b)≤2得到﹣3≤a+b≤1且﹣3≤ba≤1﹣,进一步求出|a|+|b|的求值.解答:解:(1)由已知可得f(1)=1+a+b,f(﹣1)=1a+b﹣,对称轴为x=﹣,因为|a|≥2,所以或≥1,所以函数f(x)在[1﹣,1]上单调,所以M(a,b)=max{|f(1),|f(﹣1)|}=max{|1+a+b|,|1a+b|}﹣,所以M(a,b)≥(|1+a+b|+|1a+b|﹣)≥|(1+a+b)﹣(1a+b﹣)|≥|2a|≥2;(2)当a=b=0时,|a|+|b|=0又|a|+|b|≥0,所以0为最小值,符合题意;又对任意x∈[1﹣,1].有﹣2≤x2+ax+b≤2得到﹣3≤a+b≤1且﹣3≤ba≤1﹣,易知|a|+|b|=max{|ab|﹣,|a+b|}=3,在b=1﹣,a=2时符合题意,所以|a|+|b|的最大值为3.点评:本题考查了二次函数闭区间上的最值求法;解答本题的关键是正确理解M(a,b)是|f(x)|在区间[1﹣,1]上的最大值,以及利用三角不等式变形. 19.(15分)考点:直线与圆锥曲线的关系.菁优网版权所有专题:创新题型;圆锥曲线中的最值与范围问题.分析:(1)由题意,可设直线AB的方程为x=my+n﹣,代入椭圆方程可得(m2+2)y22mny+n﹣22=0﹣,设A(x1,y1),B(x2,y2).可得△>0,设线段AB的中点P(x0,y0),利用中点坐标公式及其根与系数的可得P,代入直线y=mx+,可得,代入△>0,即可解出.(2)直线AB与x轴交点横坐标为n,可得SOAB△=,再利用均值不等式即可得出.解答:解:(1)由题意,可设直线AB的方程为x=my+n﹣,代入椭圆方程,可得(m2+2)y22mny+n﹣22=0﹣,设A(x1,y1),B(x2,y2).由题意,△=4m2n24﹣(m2+2)(n22﹣)=8(m2n﹣2+2)>0,设线段AB的中点P(x0,y0),则.x0=m×﹣+n=,由于点P在直线y=mx+上,∴=+,∴,代入△>0,可得3m4+4m24﹣>0,解得m2,∴或m.(2)直线AB与x轴交点纵坐标为n,S∴OAB△==|n|•=,由均值不等式可得:n2(m2n﹣2+2)=,S∴AOB△=,当且仅当n2=m2n﹣2+2,即2n2=m2+2,又∵,解得m=,当且仅当m=时,SAOB△取得最大值为.点评:本题考查了椭圆的定义标准方程及其性质、直线与椭圆相交问题转化为方程联立可得根与系数的关系、中点坐标公式、线段垂直平分线的性质、三角形面积计算公式、弦长公式、均值不等式的性质,考查了推理能力与计算能力,属于难题.20.(15分)考点:数列的求和;数列与不等式的综合.菁优网版权所有专题:创新题型;点列、递归数列与数学归纳法.分析:(1)通过题意易得0<an≤(n∈N*),利用ana﹣n+1=可得≥1,利用==≤2,即得结论;(2)通过=ana﹣n+1累加得Sn=a﹣n+1,利用数学归纳法可证明≥an≥(n≥2),从而≥≥,化简即得结论.解答:证明:(1)由题意可知:0<an≤(n∈N*),又∵a2=a1﹣=,∴==2,又∵ana﹣n+1=,∴an>an+1,∴≥1,∴==≤2,1≤∴≤2(n∈N*);(2)由已知,=ana﹣n+1,=an1﹣a﹣n,…,=a1a﹣2,累加,得Sn=++…+=a1a﹣n+1=a﹣n+1,易知当n=1时,要证式子显然成立;当n≥2时,=.下面证明:≥an≥(n≥2).易知当n=2时成立,假设当n=k时也成立,则ak+1=﹣+,由二次函数单调性知:an+1≥﹣+=≥,an+1≤﹣+=≤,∴≤≤,即当n=k+1时仍然成立,故对n≥2,均有≥an≥,∴=≥≥=,即(n∈N*).点评:本题是一道数列与不等式的综合题,考查数学归纳法,对表达式的灵活变形是解决本题的关键,注意解题方法的积累,属于难题.










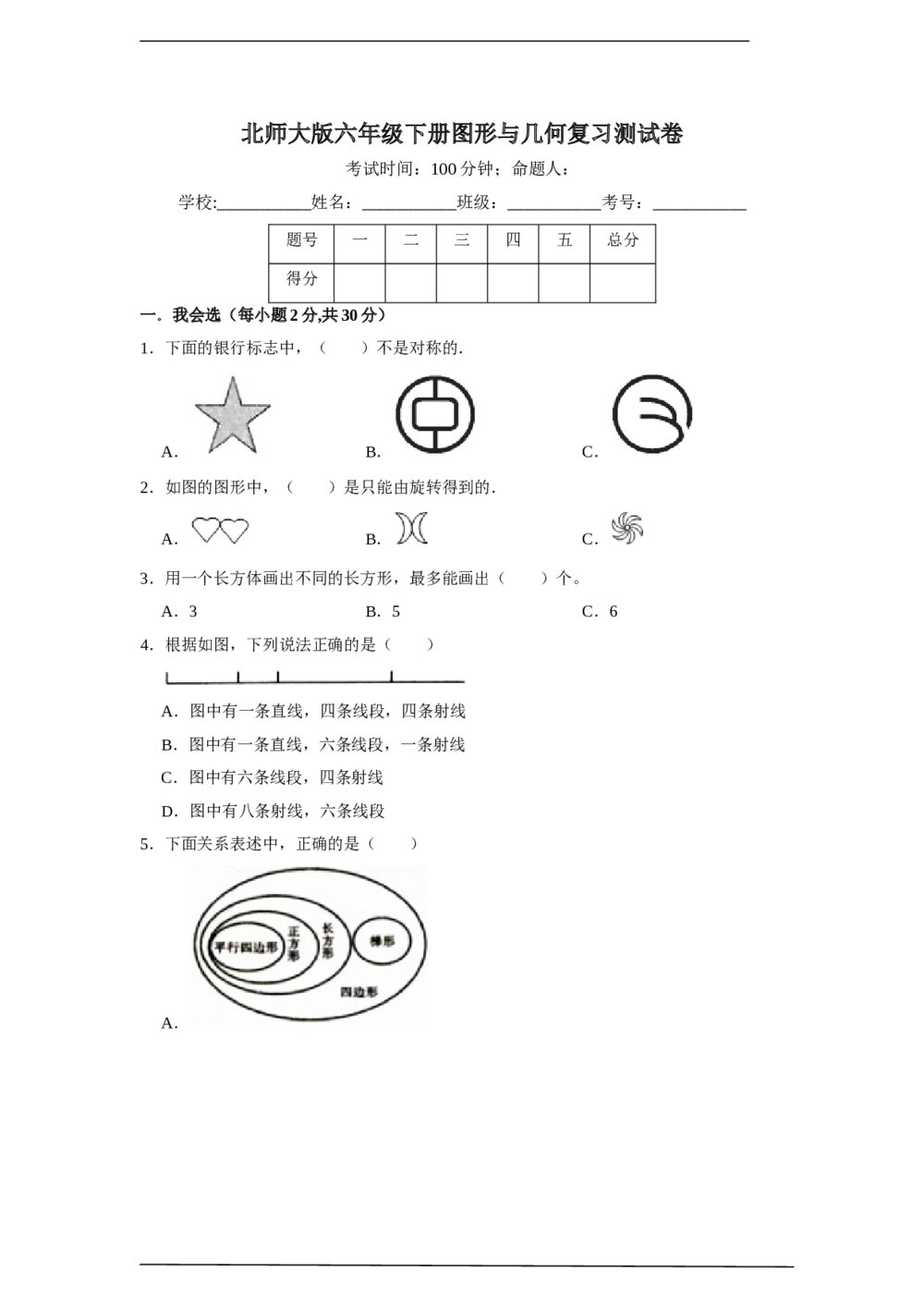 北师大版六年级数学下册图形与几何复习测试卷word版+(答案)
北师大版六年级数学下册图形与几何复习测试卷word版+(答案) 2015东北三省三校第一次模拟联考数学(文科)试题+参考答案
2015东北三省三校第一次模拟联考数学(文科)试题+参考答案 广东省汕头市2012届高三下学期二次模拟试题(文科)数学+参考答案
广东省汕头市2012届高三下学期二次模拟试题(文科)数学+参考答案 2012新课标文科数学回归教材《7不等式》
2012新课标文科数学回归教材《7不等式》 七年级数学上册《第4章 几何图形初步》单元测试卷word版无答案
七年级数学上册《第4章 几何图形初步》单元测试卷word版无答案![六年级数学奥数《第四讲[1]几何-平面部分》教师版](https://img.banbaow.com/uploadfile/2023/0531/0d3efc87daa1f139531e7/0.jpg) 六年级数学奥数《第四讲[1]几何-平面部分》教师版
六年级数学奥数《第四讲[1]几何-平面部分》教师版